Emanuele Minotto’s Blog

Link Analysis Ranking

math , search-engine , university

Some years ago I found myself making a small seminar for the course Algorithms and Data Structures II, having had very conceptual explain it in half an hour.

The goal of Link Analysis Ranking algorithms consists in inferring the importance of a web page based on the topological structure of the graph of the World Wide Web. Link analysis ranking algorithms are widely used by search engines to make the sort of web pages.

The web is then represented by a graph in which the nodes represent the HTML pages and anchors are the links between pages (indicated by the anchor <a href='...'>), each node points to zero or more links (forward links) and is pointed by zero or more links (backward links).

Crawling

Given the enormous number of pages on the World Wide Web (about 14.45 billion of the estimated pages 18/05/2011 09:03) you need to visit with a breadth-first search starting from some known nodes, deleting loops of each page, removing multiple links from one node to another node and avoid cycles between pages, redirects and temporary indexing pages.

Placing every URL visited in a stack and resolving relative URLs you discover you can avoid the first two problems listed, obviously given the elaborate nature of the problems related to the view are numerous.

Hyper Search

Developed by Massimo Marchiori in 1997, was the first to assign a value to the pages not only based on the content of the page but also evaluating its relationship with the other pages (forward links) and like the other pages linking to it (backward links).

PageRank

Developed by Lawrence Page and Sergey Brin during a research project at Stanford in 1998, is conceptually in assessing the importance of a node based on the importance of the nodes that have a link with the latter.

Algorithm

PageRank is developed on the following points:

1. generation of the adjacency matrix of the nodes
2. normalization of the rows for the number of outgoing links from the node under consideration, thus generating a stochastic matrix
3. inclusion of a “damping factor” indicating the probability that a user visiting the graph at random and coming to a node without external connections “jumps” to another randomly chosen node of the graph, this damping factor is given by \(\frac{1 - d}{n}\) where \(n\) is the total number of nodes in the graph and in the case of Google is estimated at \(0.85\) (probability that a user follows a link of the page)
4. we calculate the transpose of the matrix to obtain the rows inbound links for each node
5. we calculate the eigenvector with the power method , and being a Markov matrix we have only two classes of eigenvalues ​​, less than 1, or 1. In this case we take into account the eigenvalue to 1 as it demonstrates that the probability distribution is stabilized
6. finally, each component is associated dell’autovettore to the node under consideration

Hyperlink-Induced Topic Search

Developed by Jon Kleinberg and contemporary PageRank, is to assign a value to each node of authority and a value of hubs.

The value of the hub is given by the sum of the authority with which each node has a connection and indicates the value of the node as a pointer to authoritative sources (hubs pointing to authority), the value of authority is given by the sum of the values ​​of hub that have a link to the latter and indicates the quality of the node.

This algorithm is then symmetrical, in the sense that both the weights of a node are defined by the same method and if the lines are reversed arcs weights are reversed.

And egalitarian: when calculating the value of a hub node, the values ​​of authority aimed hub are recalculated.

Similar to this is the Hub-Averaging algorithm (HubAvg), in which the values ​​are calculated as nell’HITS of authority, but the value as the hub of a node is the average of the values ​​of the authority of the nodes to which it points.

The HITS and the HubAvg have, however, a few flaws:

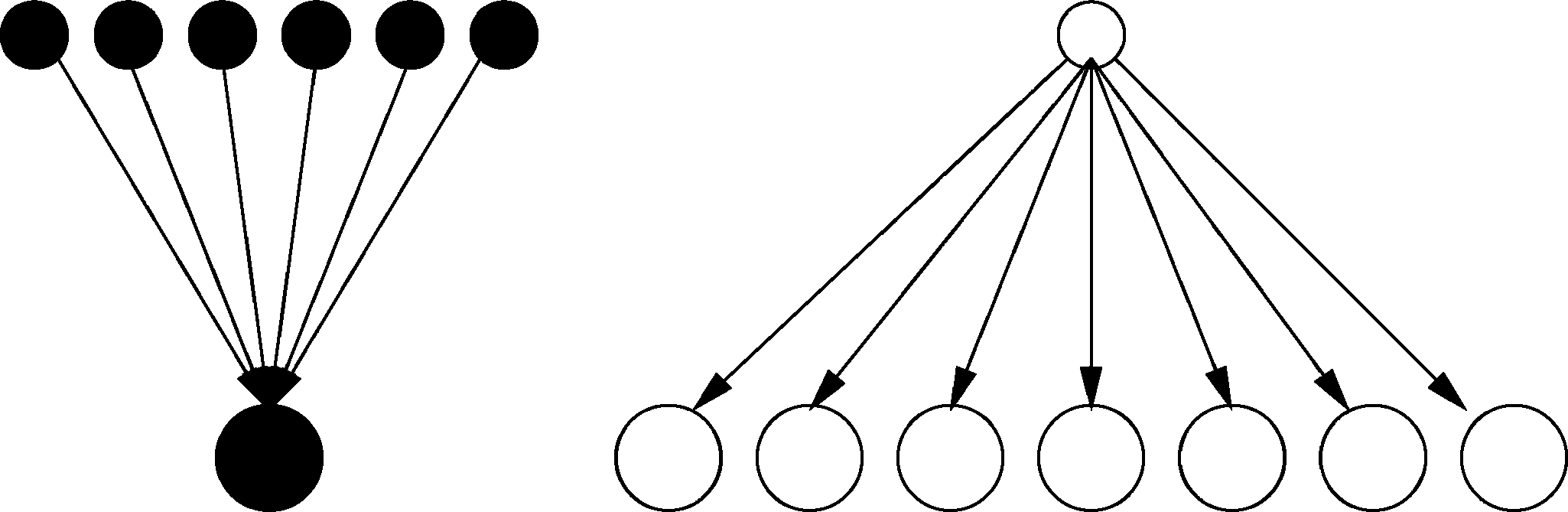
With HITS if many nodes with small hubs pointing to the same node, this will still have a high value of authority, just because defined as summation.

In the example defined above nodes are hubs, those below the authority when the number of authority white is higher than the number of hubs blacks, the algorithm assigns the authority white all the weight of authority, while the authority black to 0, this is because the hub white is rated as best hub, then the value of white authority will increase accordingly.

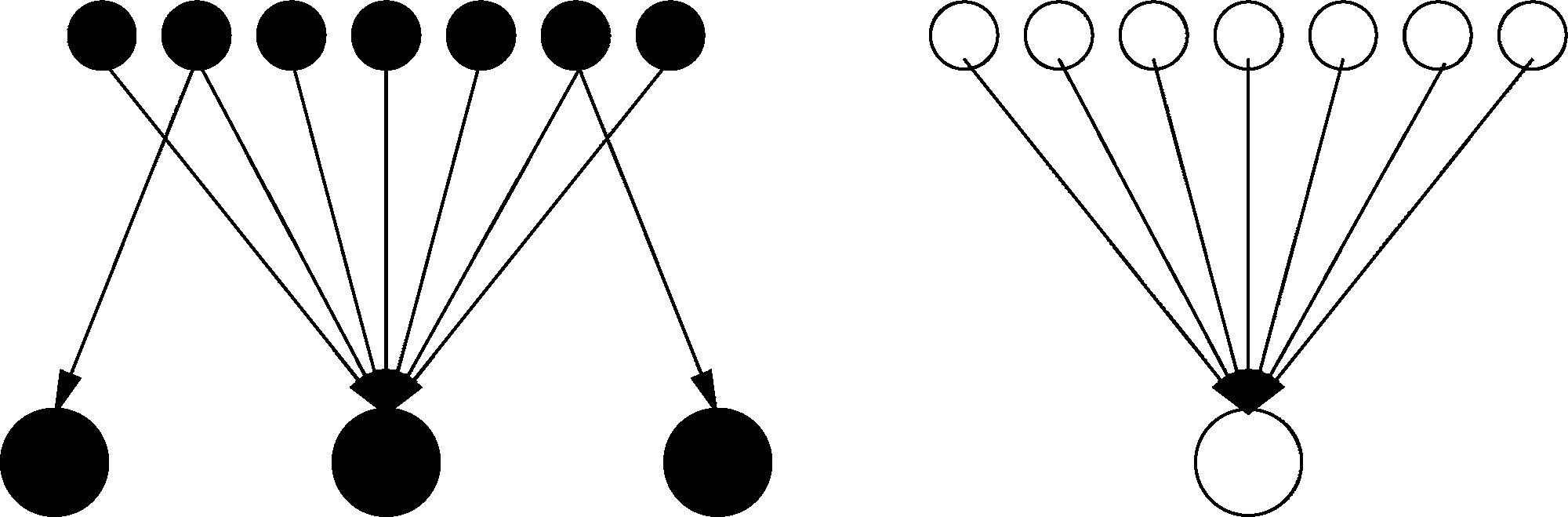
In this case however, using the HubAvg algorithm, we would obtain that the white authorities value is greater than the values ​​of authority black, this is caused by the authority black bets from a few hubs, and then recursively influential on the rest of the graph, reducing the value the authority of the central node.